Difference between revisions of "Parking of robots in Remotely-operated laboratory"
m |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | == Detekcia uhla šípky == | |
| − | + | Roboty majú na sebe farebné šípky, ktoré sú v neštandardných farbách - farby by mali byť originálne a šípky dostatočne rozmerné, aby neprišlo ku nesprávnemu určeniu prekážky, alebo časti obrázka ako šípky robota. | |
| − | + | === Postup detekcie šípok === | |
| − | - | + | *1. načitanie JPG fotografie (v RGB) |
| + | *2. prevod fotografie do HSV | ||
| + | *3. odfiltrovanie farieb mimo minHSV a maxHSV hodnôt farby šípky - vzniká binárny obrázok | ||
| + | *4. nájdenie cv contour (nerastrovo reprezentovaná krivka popisujúca jeden tvar po obvode) | ||
| + | *5. odfiltrovanie príliš malých contours, ktoré nemôžu byť naša šípka (umožňuje mať rozmedzie minHSV-maxHSV väčšie) | ||
| + | *6. aproximovanie do trojuholníka (a odfiltrovanie iných polygónov ako tých s troma vrcholmi) | ||
| − | + | ==== openCV ==== | |
| − | + | Táto knižnica poskytuje veľa užitočných funkcií, napr. konverziu obrázka z RGB do HSV, funkciu approxPolyDP() a pod. V ukážkach budú často funkcie z tejto knižnice. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==== HSV ==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Tento farebný model (Hue, Saturation, Value(Brightness) - Tón, Sýtosť, Hodnota(Jas)) bol zvolený preto, lebo jednotlivé šípky sa medzi sebou líšia najmä tónom farby a svetelné podmienky je možné popísať sýtosťou a jasom. Pri použití modelu RGB je teoreticky možné dosiahnúť rovnako dobré výsledky (medzi RGB a HSV sa dá konvertovať oboma smermi), no testovanie by bolo omnoho pomalšie. | |
| + | <source lang="cpp"> | ||
| + | // orange | ||
| + | Scalar MIN_ORANGE_HSV = getHSV(18,50,55); // 0..359, 0..100, 0..100 | ||
| + | Scalar MAX_ORANGE_HSV = getHSV(40,86,66); | ||
| − | + | // purple | |
| + | Scalar MIN_PURPLE_HSV = getHSV(315,35,40); | ||
| + | Scalar MAX_PURPLE_HSV = getHSV(359,70,54); | ||
| − | + | Mat imageRGB; | |
| + | Mat imageHSV; | ||
| + | cvtColor(imageRGB, imageHSV, CV_BGR2HSV); | ||
| + | </source> | ||
| − | [[Image: | + | ==== Filtrovanie farieb ==== |
| + | |||
| + | minHSV a maxHSV sú Scalar(int, int, int) s tromi hodnotami (HSV). Dôležité je spomenúť, že openCV má formát/rozmedzia pre HSV 0..179, 0..255, 0..255. Moja funkcia getHSV() prevádza štandardnejšie rozmedzia 0..359, 0..100, 0..100 (používané aj grafickými editormi) do openCV formátu. | ||
| + | <source lang="cpp"> | ||
| + | Mat imageHSV; | ||
| + | Mat filtered; | ||
| + | inRange(imageHSV, minHSV, maxHSV, filtered); | ||
| + | </source> | ||
| + | |||
| + | ==== Detekcia contour ==== | ||
| + | |||
| + | <source lang="cpp"> | ||
| + | vector<vector<Point> > contours; | ||
| + | vector<Vec4i> hierarchy; | ||
| + | findContours(filtered.clone(), contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_SIMPLE, Point(0, 0)); | ||
| + | </source> | ||
| + | |||
| + | Viac sa je možné dočítať v oficiálnej openCV dokumentácií s tutoriálom: http://docs.opencv.org/doc/tutorials/imgproc/shapedescriptors/find_contours/find_contours.html | ||
| + | |||
| + | Spomenutý tutorál využíva Canny operator, ktorý detekuje okraje objektov. V tomto projekte som tiež experimentoval s Canny operatorom, no výsledky neboli uspokojivé. Na obrázku nižšie je obrázok po aplikovaní Canny operatora a obrázok po odfiltrovaní nežiadúcich HSV farieb cez funkciu inRange(). | ||
| + | |||
| + | ==== Aproximácia trojuholníka ==== | ||
| + | |||
| + | <source lang="cpp"> | ||
| + | vector<Point> getTriangleVertices(const vector< vector<Point> >& contours, int minTriangleArea=0) | ||
| + | { | ||
| + | vector<Point> approxTriangle; | ||
| + | vector<Point> allTriangleVertices; | ||
| + | for(size_t i = 0; i < contours.size(); i++) // contours[i] je jedna kontúra - krivka obkreslujúca nejaký tvar | ||
| + | { | ||
| + | if (fabs(contourArea(contours[i])) < minTriangleArea) continue; // odfiltrovanie tvarov s príliš malou plochou, náš trojuholník ma plochu cca 450-480px | ||
| + | approxPolyDP(contours[i], approxTriangle, arcLength(Mat(contours[i]), true)*0.05, true); // viac tu: http://opencv.willowgarage.com/documentation/cpp/structural_analysis_and_shape_descriptors.html#cv-approxpolydp | ||
| + | if(approxTriangle.size() == 3) // chceme iba trojuholníky | ||
| + | { | ||
| + | copy(approxTriangle.begin(), approxTriangle.end(), back_inserter(allTriangleVertices)); | ||
| + | } | ||
| + | } | ||
| + | return allTriangleVertices; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | === Určenie uhlu === | ||
| + | |||
| + | <source lang="cpp"> | ||
| + | double getRobotAngle(vector<Point>& triangle); | ||
| + | </source> | ||
| + | Zo získaného trojuholníka zavolaním vlastnej funkcie dostaneme uhol trojuholníka/šípky v radiánoch. | ||
| + | |||
| + | Algoritmus funguje tak, že sa zistí najdlhšia hrana v trojuholníku a zistí sa jej uhol. Výsledný uhol šípky získame otočením ešte o 90°. Keďže som výpočty neurobil dosť matematicky "univerzálne", musel som si napísať pomocnú funkciu, którá zistí vzájomnú polohu tretieho bodu a priamky/hrany a opraviť tak prípadný preklopený uhol o 180°. | ||
| + | |||
| + | === Výsledok === | ||
| + | |||
| + | Ešte jedna funkcia, void drawShape(vector<Point> vector, Mat& img, String label); a máme to vizualizované: | ||
| + | |||
| + | [[Image:Anglerecog1.png]] | ||
| + | |||
| + | [[Image:Anglerecog2.png]] | ||
| + | |||
| + | Pri nasvietení lampou bolo však potrebné urobiť ďalšie úpravy minHSV a maxHSV: | ||
| + | |||
| + | [[Image:Anglerecog3.png]] | ||
| + | |||
| + | Potom bol výsledok lepší, aj keď vrcholy ovplyvnené neboli: | ||
| + | |||
| + | [[Image:Anglerecog3b.png]] | ||
| + | |||
| + | Výsledné uhly nie sú najpresnejšie (nepresnosť je väčšia ako 0,5°), no pri takom algoritme parkovania, ktorý priebežne zisťuje uhol robota, to nemusí byť problém. | ||
| + | |||
| + | Na pôvodný, kvalitný a širokouhlý obraz vychádzajúci z kamery je aplikovaná korekcia skreslenia, čo prispieva ku strate ostrosti hrán šípky. Riešením na zlepšenie môže byť zostrenie hrán, nastevenie väčšej citlivosti HSV filtra, alebo presná/strojová analýza farieb šipky (terajšie hodnoty minHSV a maxHSV boli odmerané ručne cez grafický editor). | ||
| + | |||
| + | == Parkovanie robota == | ||
| + | |||
| + | Parkovanie robota nebolo celkovo otestované (výpočty uhlov boli otestované vizuálne v Delphi aplikácii) a popisuje iba jednoduchý algoritmus zaparkovania. | ||
| + | |||
| + | *1. príchod pred nabíjací box | ||
| + | *2. doparkovanie do nabíjacieho boxu | ||
| + | |||
| + | === Príchod pred nabíjací box === | ||
| + | <source lang="cpp"> | ||
| + | // pozicia pred nabijacim boxom | ||
| + | double destX = 175; | ||
| + | double destY = 160; | ||
| + | |||
| + | double required_distance = 5; // odchylka vzdialenosti ciela a robota | ||
| + | double fd_step = 20; // krok dopredu na kazdu iteraciu | ||
| + | double wait_time = 200; // cakanie pri kazdej iteracii | ||
| + | int counter = 0; | ||
| + | int max_counter = 50000; // aby sa navzdy nezacyklil | ||
| + | |||
| + | // dostanie sa do destX, destY | ||
| + | |||
| + | while(1){ | ||
| + | cv::Mat src_rgb = loadImage("img.jpg"); | ||
| + | |||
| + | if (!src_rgb.data){ | ||
| + | cout << "No image\n"; | ||
| + | return 2; | ||
| + | } | ||
| + | |||
| + | vector<Point> purple_arrow = findArrow(src_rgb, MIN_PURPLE_HSV, MAX_PURPLE_HSV, 300); // posledný parameter je min obsah šípky | ||
| + | |||
| + | if (purple_arrow.size()!=3) continue; // ak sa nedetekoval žiadny trojuholník | ||
| + | |||
| + | double robot_angle_deg = getClockAngle(radToDeg(getRobotAngle(purple_arrow))); // uhol robota v rozmedzí 0..359 | ||
| + | |||
| + | Point robot_position = getCenterPoint(getLongestTriangleEdge(purple_arrow)); | ||
| + | |||
| + | double direction_deg = getClockAngle(radToDeg(PI-atan2((destX-robot_position.x),(destY-robot_position.y)))); // uhol od robota ku cielu, 0..359 | ||
| + | |||
| + | double difference_deg = direction_deg - robot_angle_deg; // rozdiel uhlov, kladny znamena rl, zaporny lt | ||
| − | + | if (difference_deg>180) difference_deg = -(180-(difference_deg-180)); // aby sa otacal cez kratsi uhol | |
| − | - | ||
| − | + | robot_rt(r, difference_deg*rotation_step); | |
| − | + | robot_fd(r, fd_step); | |
| − | + | sleep(wait_time); | |
| − | + | counter++; if (counter>=max_counter) break; // proti zacykleniu | |
| − | + | if (dist(destX,destY,robot_position.x,robot_position.y) <= required_distance) break; // je v cieli s required_distance presnostou | |
| + | } | ||
| + | </source> | ||
| − | + | === Doparkovanie robota === | |
| + | Doparkovanie robota je veľmi podobné, stačí zvoliť destY = 55; (stred boxu) a opakovať jednu iteráciu cyklu spomenutého vyššie. | ||
| − | + | == Iná práca == | |
| − | + | === Motor schema === | |
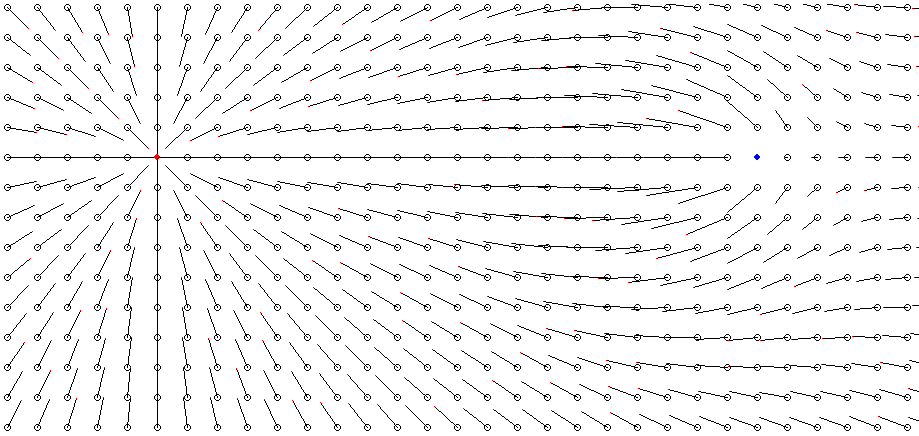
| − | + | Pôvodne zámer ako zaparkovať robota do nabíjacieho boxu bol využiť motor schema move-to-goal a avoid-obstacles. Zdá sa to ako dobrý a univerzálny spôsob pohybu robotov. V Jave som vytvoril triedy (aj ako Applet), ktorý simuluje 2D svet (napr. obrázok) s objektami rôznej, kladnej alebo zápornej, gravitácie. Schéma (reprezentácia sveta/obrázka) pozná v každom svojom bode silu pôsobiacu na tento bod zo všetkých objektov s gravitáciou. Sily sa skladajú štandardne vektorovo. Je možné ľahko pridávať objekty s gravitáciou, čím sa automaticky aktualizuje celá schéma. Táto aplikácia má nastaviteľnú presnosť, v najlepšom prípade 1px obrázka = 1bod schémy (teda pre každý pixel bude počítaná gravitácia). Je využiteľná pri move-to-goal a avoid-obstacles pohyboch takým spôsobom, že na miesto ciela sa vloží objekt s kladnou gravitáciou a na miesto prekážok sa vloží objekt so zápornou gravitáciou. Podľa výslednej schémy by bolo možné robota usmerňovať. | |
| − | + | <source lang="java"> | |
| + | s = new Schema(resolutionX, resolutionY, imgWidht, imgdHeight); | ||
| + | s.addObject(new Objekt(posX1, posY1, gravity, Double.MAX_VALUE, "DESTIN1")); // pritazlivy objekt s gravitaciou gravity a s nekonecnym dosahom | ||
| + | s.addObject(new Objekt(posX2, posY2, -gravity, gravityRadius, "OBSTAC1")); // odpudivy objekt so zapornou gravitaciou a s gravityRadius dosahom (slabne so vzdialenostou) | ||
| + | </source> | ||
| − | + | [[Image:Viz2.png]] | |
| − | + | === Artificial neural network === | |
| − | + | Pôvodne sa natočenie šípok malo detekovať neurónovou sieťou, s využitím knižnice FANN. http://leenissen.dk/fann/wp/help/getting-started/ | |
| − | + | Príklad pattern recognition: http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html#Pattern%20Recognition%20-%20an%20example | |
| − | + | Vyskúšal som NeurophStudio (http://neuroph.sourceforge.net/image_recognition.html) postavené na Eclipse. Dovoluje jednoducho a bez programovania trénovať a testovať neurónovú sieť. | |
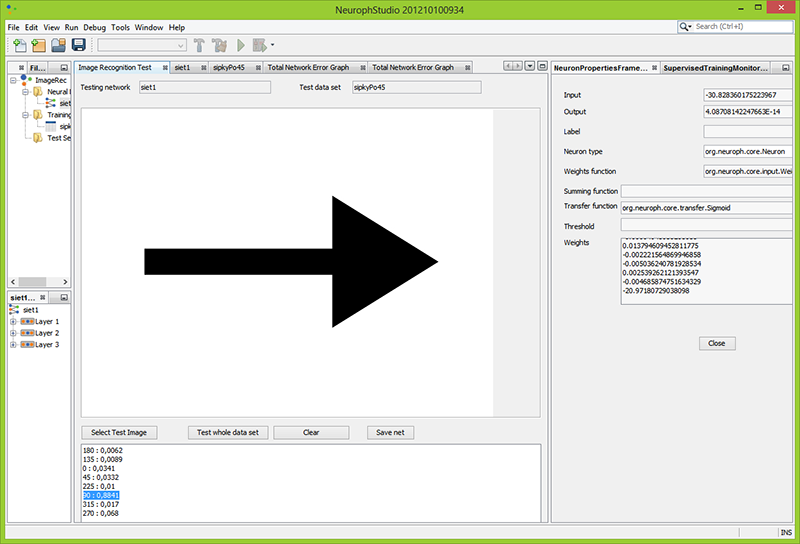
| − | + | Testovanie 90° šípky pro trénovaní s viac-menenej defaultnými parametrami vyšlo takto: | |
| + | <pre>Stupne : output | ||
| + | 180 : 0,0062 | ||
| + | 135 : 0,0089 | ||
| + | 0 : 0,0341 | ||
| + | 45 : 0,0332 | ||
| + | 225 : 0,01 | ||
| + | 90 : 0,8841 | ||
| + | 315 : 0,017 | ||
| + | 270 : 0,068</pre> | ||
[[Image:JavaNeuralNetworkimg1.png]] | [[Image:JavaNeuralNetworkimg1.png]] | ||
[[Image:JavaNeuralNetworkimg2.png]] | [[Image:JavaNeuralNetworkimg2.png]] | ||
| + | |||
| + | == Download == | ||
| + | [[Media:Proj_parkovanie_rozpoznavanie.zip|Detekcia uhla šípky]] | ||
| + | |||
| + | [[Media:Proj_parkovanie_parkovanie.cpp|Parkovanie robota]] | ||
| + | |||
| + | [[Media:Proj_parkovanie_java_schema.zip|Schema v Jave]] | ||
Latest revision as of 14:48, 28 June 2013
Detekcia uhla šípky
Roboty majú na sebe farebné šípky, ktoré sú v neštandardných farbách - farby by mali byť originálne a šípky dostatočne rozmerné, aby neprišlo ku nesprávnemu určeniu prekážky, alebo časti obrázka ako šípky robota.
Postup detekcie šípok
- 1. načitanie JPG fotografie (v RGB)
- 2. prevod fotografie do HSV
- 3. odfiltrovanie farieb mimo minHSV a maxHSV hodnôt farby šípky - vzniká binárny obrázok
- 4. nájdenie cv contour (nerastrovo reprezentovaná krivka popisujúca jeden tvar po obvode)
- 5. odfiltrovanie príliš malých contours, ktoré nemôžu byť naša šípka (umožňuje mať rozmedzie minHSV-maxHSV väčšie)
- 6. aproximovanie do trojuholníka (a odfiltrovanie iných polygónov ako tých s troma vrcholmi)
openCV
Táto knižnica poskytuje veľa užitočných funkcií, napr. konverziu obrázka z RGB do HSV, funkciu approxPolyDP() a pod. V ukážkach budú často funkcie z tejto knižnice.
HSV
Tento farebný model (Hue, Saturation, Value(Brightness) - Tón, Sýtosť, Hodnota(Jas)) bol zvolený preto, lebo jednotlivé šípky sa medzi sebou líšia najmä tónom farby a svetelné podmienky je možné popísať sýtosťou a jasom. Pri použití modelu RGB je teoreticky možné dosiahnúť rovnako dobré výsledky (medzi RGB a HSV sa dá konvertovať oboma smermi), no testovanie by bolo omnoho pomalšie.
// orange
Scalar MIN_ORANGE_HSV = getHSV(18,50,55); // 0..359, 0..100, 0..100
Scalar MAX_ORANGE_HSV = getHSV(40,86,66);
// purple
Scalar MIN_PURPLE_HSV = getHSV(315,35,40);
Scalar MAX_PURPLE_HSV = getHSV(359,70,54);
Mat imageRGB;
Mat imageHSV;
cvtColor(imageRGB, imageHSV, CV_BGR2HSV);
Filtrovanie farieb
minHSV a maxHSV sú Scalar(int, int, int) s tromi hodnotami (HSV). Dôležité je spomenúť, že openCV má formát/rozmedzia pre HSV 0..179, 0..255, 0..255. Moja funkcia getHSV() prevádza štandardnejšie rozmedzia 0..359, 0..100, 0..100 (používané aj grafickými editormi) do openCV formátu.
Mat imageHSV;
Mat filtered;
inRange(imageHSV, minHSV, maxHSV, filtered);
Detekcia contour
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(filtered.clone(), contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_SIMPLE, Point(0, 0));
Viac sa je možné dočítať v oficiálnej openCV dokumentácií s tutoriálom: http://docs.opencv.org/doc/tutorials/imgproc/shapedescriptors/find_contours/find_contours.html
Spomenutý tutorál využíva Canny operator, ktorý detekuje okraje objektov. V tomto projekte som tiež experimentoval s Canny operatorom, no výsledky neboli uspokojivé. Na obrázku nižšie je obrázok po aplikovaní Canny operatora a obrázok po odfiltrovaní nežiadúcich HSV farieb cez funkciu inRange().
Aproximácia trojuholníka
vector<Point> getTriangleVertices(const vector< vector<Point> >& contours, int minTriangleArea=0)
{
vector<Point> approxTriangle;
vector<Point> allTriangleVertices;
for(size_t i = 0; i < contours.size(); i++) // contours[i] je jedna kontúra - krivka obkreslujúca nejaký tvar
{
if (fabs(contourArea(contours[i])) < minTriangleArea) continue; // odfiltrovanie tvarov s príliš malou plochou, náš trojuholník ma plochu cca 450-480px
approxPolyDP(contours[i], approxTriangle, arcLength(Mat(contours[i]), true)*0.05, true); // viac tu: http://opencv.willowgarage.com/documentation/cpp/structural_analysis_and_shape_descriptors.html#cv-approxpolydp
if(approxTriangle.size() == 3) // chceme iba trojuholníky
{
copy(approxTriangle.begin(), approxTriangle.end(), back_inserter(allTriangleVertices));
}
}
return allTriangleVertices;
}
Určenie uhlu
double getRobotAngle(vector<Point>& triangle);
Zo získaného trojuholníka zavolaním vlastnej funkcie dostaneme uhol trojuholníka/šípky v radiánoch.
Algoritmus funguje tak, že sa zistí najdlhšia hrana v trojuholníku a zistí sa jej uhol. Výsledný uhol šípky získame otočením ešte o 90°. Keďže som výpočty neurobil dosť matematicky "univerzálne", musel som si napísať pomocnú funkciu, którá zistí vzájomnú polohu tretieho bodu a priamky/hrany a opraviť tak prípadný preklopený uhol o 180°.
Výsledok
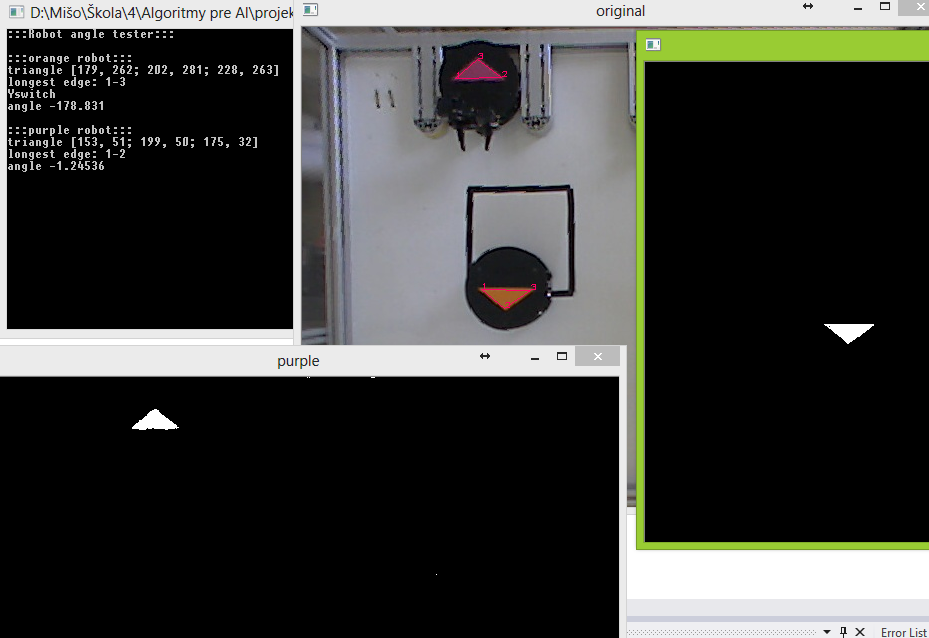
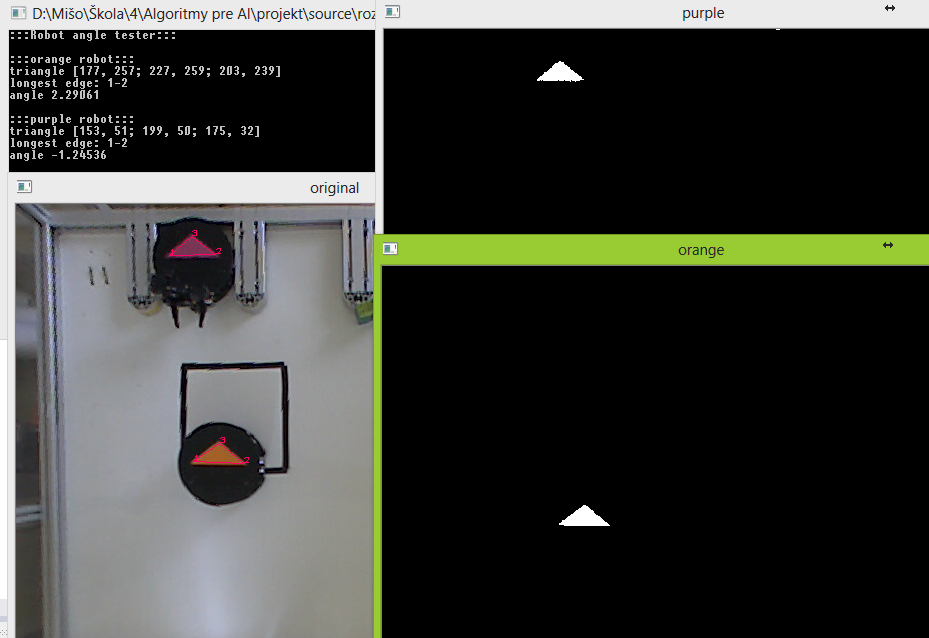
Ešte jedna funkcia, void drawShape(vector<Point> vector, Mat& img, String label); a máme to vizualizované:
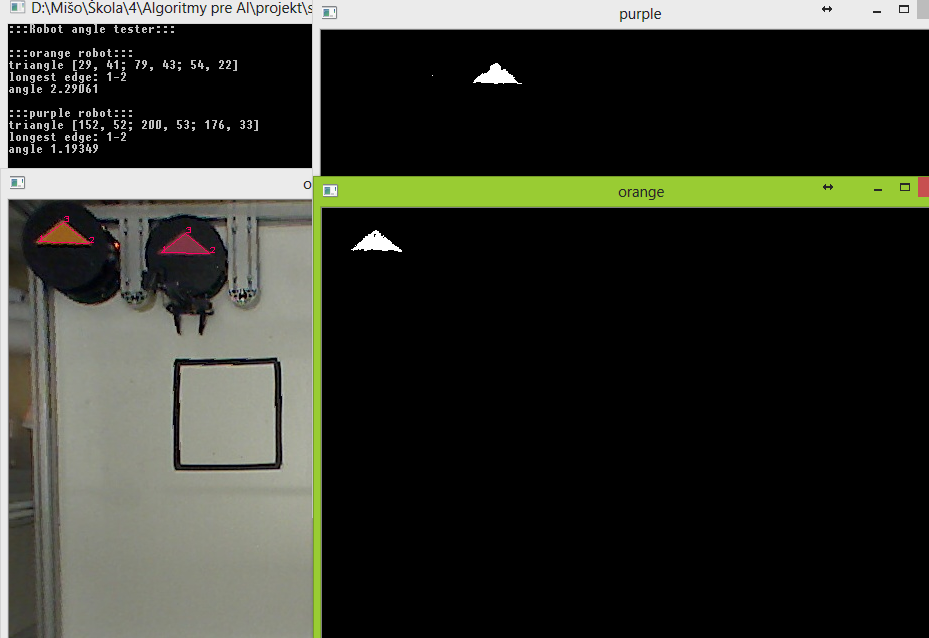
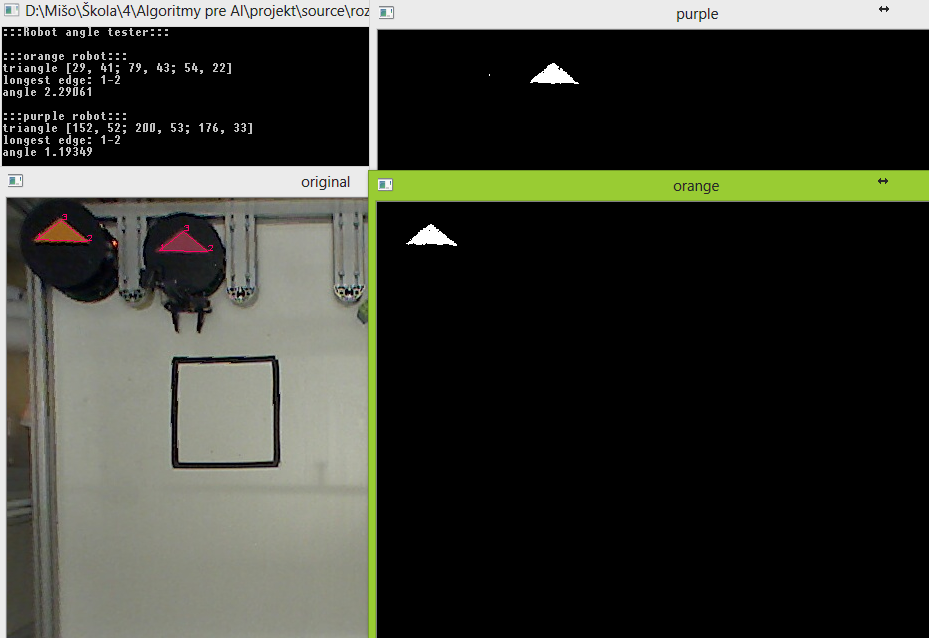
Pri nasvietení lampou bolo však potrebné urobiť ďalšie úpravy minHSV a maxHSV:
Potom bol výsledok lepší, aj keď vrcholy ovplyvnené neboli:
Výsledné uhly nie sú najpresnejšie (nepresnosť je väčšia ako 0,5°), no pri takom algoritme parkovania, ktorý priebežne zisťuje uhol robota, to nemusí byť problém.
Na pôvodný, kvalitný a širokouhlý obraz vychádzajúci z kamery je aplikovaná korekcia skreslenia, čo prispieva ku strate ostrosti hrán šípky. Riešením na zlepšenie môže byť zostrenie hrán, nastevenie väčšej citlivosti HSV filtra, alebo presná/strojová analýza farieb šipky (terajšie hodnoty minHSV a maxHSV boli odmerané ručne cez grafický editor).
Parkovanie robota
Parkovanie robota nebolo celkovo otestované (výpočty uhlov boli otestované vizuálne v Delphi aplikácii) a popisuje iba jednoduchý algoritmus zaparkovania.
- 1. príchod pred nabíjací box
- 2. doparkovanie do nabíjacieho boxu
Príchod pred nabíjací box
// pozicia pred nabijacim boxom
double destX = 175;
double destY = 160;
double required_distance = 5; // odchylka vzdialenosti ciela a robota
double fd_step = 20; // krok dopredu na kazdu iteraciu
double wait_time = 200; // cakanie pri kazdej iteracii
int counter = 0;
int max_counter = 50000; // aby sa navzdy nezacyklil
// dostanie sa do destX, destY
while(1){
cv::Mat src_rgb = loadImage("img.jpg");
if (!src_rgb.data){
cout << "No image\n";
return 2;
}
vector<Point> purple_arrow = findArrow(src_rgb, MIN_PURPLE_HSV, MAX_PURPLE_HSV, 300); // posledný parameter je min obsah šípky
if (purple_arrow.size()!=3) continue; // ak sa nedetekoval žiadny trojuholník
double robot_angle_deg = getClockAngle(radToDeg(getRobotAngle(purple_arrow))); // uhol robota v rozmedzí 0..359
Point robot_position = getCenterPoint(getLongestTriangleEdge(purple_arrow));
double direction_deg = getClockAngle(radToDeg(PI-atan2((destX-robot_position.x),(destY-robot_position.y)))); // uhol od robota ku cielu, 0..359
double difference_deg = direction_deg - robot_angle_deg; // rozdiel uhlov, kladny znamena rl, zaporny lt
if (difference_deg>180) difference_deg = -(180-(difference_deg-180)); // aby sa otacal cez kratsi uhol
robot_rt(r, difference_deg*rotation_step);
robot_fd(r, fd_step);
sleep(wait_time);
counter++; if (counter>=max_counter) break; // proti zacykleniu
if (dist(destX,destY,robot_position.x,robot_position.y) <= required_distance) break; // je v cieli s required_distance presnostou
}
Doparkovanie robota
Doparkovanie robota je veľmi podobné, stačí zvoliť destY = 55; (stred boxu) a opakovať jednu iteráciu cyklu spomenutého vyššie.
Iná práca
Motor schema
Pôvodne zámer ako zaparkovať robota do nabíjacieho boxu bol využiť motor schema move-to-goal a avoid-obstacles. Zdá sa to ako dobrý a univerzálny spôsob pohybu robotov. V Jave som vytvoril triedy (aj ako Applet), ktorý simuluje 2D svet (napr. obrázok) s objektami rôznej, kladnej alebo zápornej, gravitácie. Schéma (reprezentácia sveta/obrázka) pozná v každom svojom bode silu pôsobiacu na tento bod zo všetkých objektov s gravitáciou. Sily sa skladajú štandardne vektorovo. Je možné ľahko pridávať objekty s gravitáciou, čím sa automaticky aktualizuje celá schéma. Táto aplikácia má nastaviteľnú presnosť, v najlepšom prípade 1px obrázka = 1bod schémy (teda pre každý pixel bude počítaná gravitácia). Je využiteľná pri move-to-goal a avoid-obstacles pohyboch takým spôsobom, že na miesto ciela sa vloží objekt s kladnou gravitáciou a na miesto prekážok sa vloží objekt so zápornou gravitáciou. Podľa výslednej schémy by bolo možné robota usmerňovať.
s = new Schema(resolutionX, resolutionY, imgWidht, imgdHeight);
s.addObject(new Objekt(posX1, posY1, gravity, Double.MAX_VALUE, "DESTIN1")); // pritazlivy objekt s gravitaciou gravity a s nekonecnym dosahom
s.addObject(new Objekt(posX2, posY2, -gravity, gravityRadius, "OBSTAC1")); // odpudivy objekt so zapornou gravitaciou a s gravityRadius dosahom (slabne so vzdialenostou)
Artificial neural network
Pôvodne sa natočenie šípok malo detekovať neurónovou sieťou, s využitím knižnice FANN. http://leenissen.dk/fann/wp/help/getting-started/
Príklad pattern recognition: http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html#Pattern%20Recognition%20-%20an%20example
Vyskúšal som NeurophStudio (http://neuroph.sourceforge.net/image_recognition.html) postavené na Eclipse. Dovoluje jednoducho a bez programovania trénovať a testovať neurónovú sieť.
Testovanie 90° šípky pro trénovaní s viac-menenej defaultnými parametrami vyšlo takto:
Stupne : output 180 : 0,0062 135 : 0,0089 0 : 0,0341 45 : 0,0332 225 : 0,01 90 : 0,8841 315 : 0,017 270 : 0,068