Difference between revisions of "GolfBot"
m |
|||
| Line 18: | Line 18: | ||
*# Vytvorí si novú kópiu obrázku (pre účely spracovania). | *# Vytvorí si novú kópiu obrázku (pre účely spracovania). | ||
*# Aplikuje gaussovo rozmazanie pracovného obrázka z polomerom 3px. | *# Aplikuje gaussovo rozmazanie pracovného obrázka z polomerom 3px. | ||
| − | *# Skonvertuje obrázok z farebného formátu | + | *# Skonvertuje obrázok z farebného formátu BGR do LAB. |
| − | *# Pomocou prahovania, nájdeniu najväčšieho spojitého komponentu a priemerovania x, y pozícií pixelov najväčšieho spoločného komponentu nájde stredy kruhových značiek | + | *# Pomocou prahovania, nájdeniu najväčšieho spojitého komponentu a priemerovania x, y pozícií pixelov najväčšieho spoločného komponentu nájde stredy kruhových značiek a lopty. |
*# Určia sa polohy cieľa (stred obrázka), lopty (oranžová značka na obrázku), polomer lopty a pozicia robota. | *# Určia sa polohy cieľa (stred obrázka), lopty (oranžová značka na obrázku), polomer lopty a pozicia robota. | ||
*# Spočíta sa uhol natočenia robota (podľa zelenej a modrej značky). | *# Spočíta sa uhol natočenia robota (podľa zelenej a modrej značky). | ||
*# Vykreslia sa získané body do náhľadového obrázka. | *# Vykreslia sa získané body do náhľadového obrázka. | ||
*# Hlavné vlákno programu je notifikované o dokončení cyklu kamery (teda sú spočítané potrebné body pre ďalšiu fázu programu hlavného vlákna). | *# Hlavné vlákno programu je notifikované o dokončení cyklu kamery (teda sú spočítané potrebné body pre ďalšiu fázu programu hlavného vlákna). | ||
| + | |||
| + | [[Image:GolfBot_Diagram_kamery.png|Diagram spracovania obrázka z kamery]] | ||
==== Gaussovo rozmazanie obrázku ==== | ==== Gaussovo rozmazanie obrázku ==== | ||
| Line 39: | Line 41: | ||
==== Prahovanie ==== | ==== Prahovanie ==== | ||
| − | Prahovanie používame na získanie | + | Prahovanie používame na získanie masky informácií o prítomnosti farebnej informácie v LAB formáte v spracovávanom obrázku. Tento algoritmus (metóda <code>prahuj(float[] from, float[] to)</code>) dostáva minimálnu a maximálnu hodnotu prahu farby v LAB formáte a v obrázku zisťuje, pre každý pixel, či je v rozsahu tejto hodnoty alebo nie je. Ak pixel v rozsahu je, dostane výstupná maska na pozícii pixelu hodnotu 1, v opačnom prípade je použitá hodnota 0. |
'''int[]''' ''o'' = '''new int['''potrebná veľkosť''']''' | '''int[]''' ''o'' = '''new int['''potrebná veľkosť''']''' | ||
| Line 52: | Line 54: | ||
==== Najväčší spojitý komponent ==== | ==== Najväčší spojitý komponent ==== | ||
| − | Výstupom z prahovania je | + | Výstupom z prahovania je maska obsahujúca nuly a jednotky, na pozíciách, kde bola zistená vhodná farba. Algoritmus nájdenia najväčšieho spojitého komponentu prehľadáva pôvodnú masku, v prípade nájdenia hodnoty jedna spustí prehľadávanie do šírky, pričom každý susedný pixel (v každom z 8 smerov) označí hodnotou N. N začína na hodnote 2 a je zvyšovaný po dokončení označenia komponentu, tento číselný údaj je vpisovaný do vstupnej masky. Tento komponent sa hľadá metódou <code>int flood(int px, int py, int[] in, int n)</code>, ktorá dostáva súradnice prvého bodu komponentu, masku a číselné označenie komponentu, označí komponent a spočíta počet pixelov v tomto komponente, ktorý následne vráti. |
| − | Každý komponent je zapísaný do <code>HashMap</code>, kde kľúč je číslo komponentu a hodnota je počet pixelov v komponente. Po nájdení všetkých komponentov sa určí najväčší z nich a | + | Každý komponent je zapísaný do <code>HashMap</code>, kde kľúč je číslo komponentu a hodnota je počet pixelov v komponente. Po nájdení všetkých komponentov sa určí najväčší z nich a maska sa opäť preznačí na hodnoty 0 a jednoa takto: |
* Ak pixel má hodnotu čísla najväčšieho komponentu, bude nastavený na hodnotu 1. | * Ak pixel má hodnotu čísla najväčšieho komponentu, bude nastavený na hodnotu 1. | ||
| Line 61: | Line 63: | ||
Metóda hľadajúca najväčší spojitý komponent má názov <code>najSpoj</code>. | Metóda hľadajúca najväčší spojitý komponent má názov <code>najSpoj</code>. | ||
| − | ==== Určenie stredu a | + | ==== Určenie stredu a AABB ohraničenia komponentu ==== |
| − | Na získanie stredu a | + | Na získanie stredu a AABB ohraničenia komponentu sa používa metóda <code>drawX</code>. Metóda dostáva masku s určeným najväčším spojitým komponentom, pričom pre každý pixel, ktorého hodnota je rovná 1, je pozícia pixelu x a y pripočítaná k ceľkovému súčtu. Rovnako sú pre každé x a y upravené hodnoty premenných <code>maxX</code>, <code>minX</code>, <code>maxY</code> a <code>minY</code>. Výsledný stred je vypočítaný ako pomer súčtu x ku počtu pixlov a súctu y k počtu pixlov. |
'''int[]''' ''stred'' = '''new int['''6''']''' | '''int[]''' ''stred'' = '''new int['''6''']''' | ||
Revision as of 17:32, 27 May 2015
GolfBot spis projektu (pripravuje sa) ...
Contents
Program
Prepojenie s kamerou a určovanie orientačných bodov
Obraz sme získavali pomocou Kinectu pre XBox 360. Máme dve triedy, Kinect (odvodená od edu.ufl.digitalworlds.j4k.J4KSDK) a Camera (implementuje Runnable).
Hlavný program spúšťa vlákno kamery, ktoré následne pri inicializácii spustí vlákno kinectu v móde J4KSDK.COLOR. Inštancii tredy Kinect je potom poslaná referencia na kameru. Trieda Kinect prekrýva metódu udalosti onColorFrameEvent, ktorá nastáva po zosnímaní farebného obrazu kinectom, pričom tento obraz posiela inštancii kamery cez referenciu volaním jej verejnej metódy setImageFromKinect.
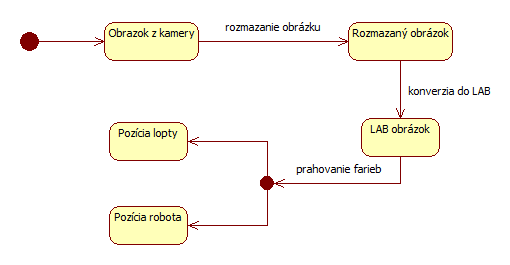
Hlavné vlákno kamery vykonáva cyklicky tieto akcie:
Najprv sa otestuje, či existuje snímka z kamery.
- Ak nie, ukončí iteráciu cyklu a pokračuje ďalšou iteráciou.
- Ak áno:
- Vytvorí si novú kópiu obrázku (pre účely spracovania).
- Aplikuje gaussovo rozmazanie pracovného obrázka z polomerom 3px.
- Skonvertuje obrázok z farebného formátu BGR do LAB.
- Pomocou prahovania, nájdeniu najväčšieho spojitého komponentu a priemerovania x, y pozícií pixelov najväčšieho spoločného komponentu nájde stredy kruhových značiek a lopty.
- Určia sa polohy cieľa (stred obrázka), lopty (oranžová značka na obrázku), polomer lopty a pozicia robota.
- Spočíta sa uhol natočenia robota (podľa zelenej a modrej značky).
- Vykreslia sa získané body do náhľadového obrázka.
- Hlavné vlákno programu je notifikované o dokončení cyklu kamery (teda sú spočítané potrebné body pre ďalšiu fázu programu hlavného vlákna).
Gaussovo rozmazanie obrázku
Na rozmazanie obrázka (blur) je použítá aproximácia gaussovho rozmazávacieho algoritmu, ktorý dokáže pracovať v lineárnom čase. Použili sme port algoritmu z JavaScriptu z blogu Ivana Kuckira, nájsť ho je možné na stránke Fastest Gaussian Blur (in linear time) (jedná sa o algoritmus 4 na tejto stránke).
Keďže algoritmus počíta s tým, že obrázok je tvorený polom bajtov, kde jeden bajt reprezentuje jeden pixel, bolo nutné obrázok rozdeliť na tri obrázky, ktoré reprezentovali jeho červenú, zelenú a modrú farebnú zložku samostatne. Potom, ako algoritmus rozmazania dokončil svoju prácu na každom z týchto rozdelených obrázkov, bolo treba ich opätovne spojiť do jedného obrázka. Na toto nám slúžia metódy separateColor a putColor.
Prevod z RGB do LAB
Keďže zosnímaný obrázok z kamery je vo formáte, kde jeden pixel je určený štyrmi bajtmi s významom: Blue, Green, Red a posledný je vždy nulový (hodnota 0), pričom tieto hodnoty sú v rozsahu od 0 do 255, je treba najprv každý pixel preformátovať do tvaru RGB, kde každá hodnota je float s hodnotou od 0 do 1. Na to máme metódu getPixel s následným predelením každej zložky hodnotou 255.
Každý pixel je potom vložený do statickej metódy triedy CIELab s názvom fromRGB, ktorá vráti hodnotu pixelu vo formáte farieb LAB. Trieda CIELab na prevod z RGB do LAB ešte používa medzikrok, kde každý RGB pixel prevedie do formátu XYZ, z ktorého následne vytvorí LAB formát.
Prahovanie
Prahovanie používame na získanie masky informácií o prítomnosti farebnej informácie v LAB formáte v spracovávanom obrázku. Tento algoritmus (metóda prahuj(float[] from, float[] to)) dostáva minimálnu a maximálnu hodnotu prahu farby v LAB formáte a v obrázku zisťuje, pre každý pixel, či je v rozsahu tejto hodnoty alebo nie je. Ak pixel v rozsahu je, dostane výstupná maska na pozícii pixelu hodnotu 1, v opačnom prípade je použitá hodnota 0.
int[] o = new int[potrebná veľkosť]
for každé x
for každé y
if pixel na x a y je medzi from a to
zapíš do o 1
else
zapíš do o 0
return o
Najväčší spojitý komponent
Výstupom z prahovania je maska obsahujúca nuly a jednotky, na pozíciách, kde bola zistená vhodná farba. Algoritmus nájdenia najväčšieho spojitého komponentu prehľadáva pôvodnú masku, v prípade nájdenia hodnoty jedna spustí prehľadávanie do šírky, pričom každý susedný pixel (v každom z 8 smerov) označí hodnotou N. N začína na hodnote 2 a je zvyšovaný po dokončení označenia komponentu, tento číselný údaj je vpisovaný do vstupnej masky. Tento komponent sa hľadá metódou int flood(int px, int py, int[] in, int n), ktorá dostáva súradnice prvého bodu komponentu, masku a číselné označenie komponentu, označí komponent a spočíta počet pixelov v tomto komponente, ktorý následne vráti.
Každý komponent je zapísaný do HashMap, kde kľúč je číslo komponentu a hodnota je počet pixelov v komponente. Po nájdení všetkých komponentov sa určí najväčší z nich a maska sa opäť preznačí na hodnoty 0 a jednoa takto:
- Ak pixel má hodnotu čísla najväčšieho komponentu, bude nastavený na hodnotu 1.
- Ak pixel má inú hodnotu, bude nastavený na 0.
Metóda hľadajúca najväčší spojitý komponent má názov najSpoj.
Určenie stredu a AABB ohraničenia komponentu
Na získanie stredu a AABB ohraničenia komponentu sa používa metóda drawX. Metóda dostáva masku s určeným najväčším spojitým komponentom, pričom pre každý pixel, ktorého hodnota je rovná 1, je pozícia pixelu x a y pripočítaná k ceľkovému súčtu. Rovnako sú pre každé x a y upravené hodnoty premenných maxX, minX, maxY a minY. Výsledný stred je vypočítaný ako pomer súčtu x ku počtu pixlov a súctu y k počtu pixlov.
int[] stred = new int[6]
long sx = 0, sy = 0
int maxX = 0, maxY = 0, minX = width, minY = height, pocet = 0
for každý x
for každý y
if pixel x,y patrí komponentu
sx += x, sy += y, pocet++
maxX = max(maxX, x)
maxY = max(maxY, y)
minX = min(minX, x)
minY = min(minY, y)
if pocet je 0
return stred
stred[0] = round(sx / pocet)
stred[1] = round(sy / pocet)
stred[2] = minX
stred[3] = minY
stred[4] = maxX
stred[5] = maxY
return stred