Difference between revisions of "Evolution with Open Dynamics Engine (Bečvarová Ľuboslava)"
(→Ukážky) |
(→Výsledky) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 41: | Line 41: | ||
== Výsledky == | == Výsledky == | ||
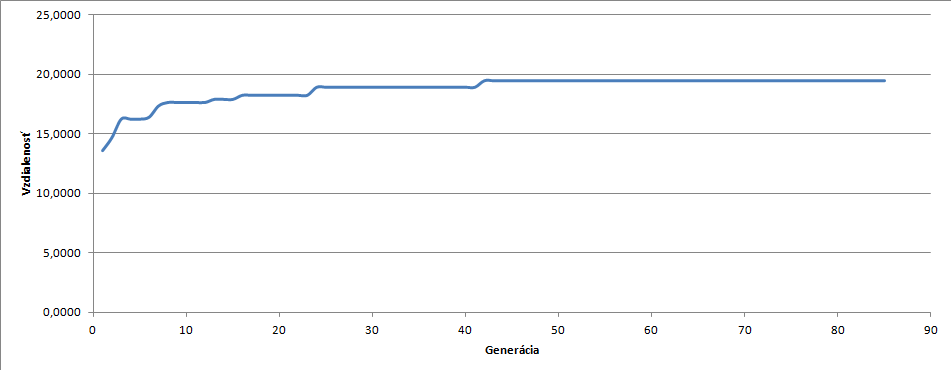
| − | Program bol pustený 12 hodín. Bol testovaný na populácií o veľkosti 100 a celkovo takto veľkých generácií bolo pustených 85. Na obrázku dobre vidno, že program začal pomerne rýchlo konvergovať a už približne v 40-tej generácií sa dostal k najlepšiemu riešeniu, aké našiel za | + | Program bol pustený približne 12 hodín. Bol testovaný na populácií o veľkosti 100 a celkovo takto veľkých generácií bolo pustených 85. Na obrázku dobre vidno, že program začal pomerne rýchlo konvergovať a už približne v 40-tej generácií sa dostal k najlepšiemu riešeniu, aké našiel za celý svoj beh. Na x-ovej osi grafu sú čísla 1 až 85, teda vieme určiť, ktorá generácia to bola. Na y-ovej osi grafu sú reálne čísla, ktoré predstavujú vzdialenosť, ktorú prešiel najlepší robot danej generácie. |
[[Image:graf.bmp]] | [[Image:graf.bmp]] | ||
| Line 67: | Line 67: | ||
== Zdrojáky == | == Zdrojáky == | ||
| − | [[Media: | + | [[Media:projekt_becvarova.zip]] |
| + | |||
| + | == Zdroje == | ||
| + | # [http://www.ode.org/ ODE] | ||
| + | # [http://lancet.mit.edu/ga/ GAlib] | ||
Latest revision as of 14:29, 14 June 2013
Contents
Úvod
Mojou úlohou bolo vytvoriť simuláciu evolúcie, kde by sme vytvorili robota, ktorému budeme ako vstup dávať tri reálne čísla, ktoré budeme neskôr používať ako sily, ktoré naňho pôsobia v rôznych smeroch. Cieľom je, aby robot dosahoval čo najväčšiu rýchlosť, teda prešiel za rovnaký čas čo najväčšiu vzdialenosť.
ODE
Pri svojej práci som použila ODE. Je to open-source knižnica, ktorá slúži na simuláciu dynamiky pevných predmetov. Knižnica je plne funkčná, stabilná, vyspelá a platformovo nezávislá, ktorá je jednoducho použiteľná s C/C++ API. Má pokročilé kĺby a integrovanú detekciu kolízií s trením. Kĺbové konštrukcia sa vytvorí, keď sú telesá rôznych tvarov spojené s kĺbmi z rôznych druhov. Príklady sú pozemné vozidlá (ak sú kolesá zapojený na kostru), bytosti s nohami (kde nohy sú pripojené k telu). ODE má zabudovaný systém detekcie kolízií. Avšak ten môžete ignorovať a robiť si vlastné detekciu kolízií, ak chcete. ODE je užitočné pre simuláciu vozidiel, objektov vo virtuálnych prostrediach alebo virtuálnych bytostí. V súčastnosti sa používa v mnohých počítačových hrách, 3D nástrojoch pre tvorbu a v simulačných nástrojoch. ODE je určený pre použitie v interaktívnych simuláciách alebo v simulácií v reálnom čase. Je zvlášť vhodná pre simuláciu pohybujúcich sa objektov v premenlivých virtuálnej realite.
GAlib
GAlib je C++ knižnica komponentov genetických algoritmov. GAlib obsahuje sadu C++ objektov genetických algoritmov. Knižnica obsahuje nástroje pre používanie genetických algoritmov na optimalizáciu v ľubovoľnom C++ programe použitím ľubovoľnej reprezentácie a genetických operátorov. Dokumentácia obsahuje rozsiahly prehľad o tom, ako realizovať genetický algoritmus, rovnako ako príklady ilustrujúce úpravy na GAlib triedy. GAlib bol postavený na rôznych platformách UNIX (Linux, MacOSX, SGI, Sun, HP, DEC, IBM), ako aj MacOS a DOS / Windows systémov. GAlib obsahuje príklady, ktoré používajú PVM pre distribuované paralelné, implementácie.
Postup
V hlavnej časti programu - vo funkcií int main(int argc, char **argv) sa na začiatku nachádzajú nastavenia veľkosti populácie, počtu generácií, pravdepodobnosť mutácie a pravdepodobnosť kríženia. Tu sa využíva knižnica GAlib. Ďalej sa vytvorí genóm. Knižnica GAlib ponúka na výber z ôsmych základných typov genómov. Niektoré z nich sa ešte delia na ďalšie typy genómov. Ja som si pre svoj projekt vybrala GA2DBinaryStringGenome. Tento typ genómu vytvorí dvojrozmerné pole binárnych čísel. Pre tento projekt vytvoríme pole veľkosti 20 krát 3. Tri preto, lebo tri položky budeme evolvovať a dvadsať znamená, že číslo sa bude skladať z dvadsiatich cifier. Tieto čísla vydelíme nakoniec konštantou 1048576.0 (2^20), aby sme nedostávali priveľké čísla. Genómu nastavíme aj jeho Objecive funkciu. Potom si konečne vytvoríme genetický algoritmus, ktorý použijeme. Pre tento projekt som zvolila GASimpleGA. Ide o "jednoduchý" genetický algoritmus, ktorý popisuje pán Goldberg vo svojej knihe. Algoritmus používa neprekrývajúce sa populácie. Pri vytváraní jednoduchého genetického algoritmu je potrebné špecifikovať buď jedinca alebo populáciu jedincov. Nový genetický algoritmus bude klonovať jedincov podľa predchádzajúcej špecifikácie na vytvorenie vlastnej populácie. Do tohto genetického algoritmu priradíme všetko, čo sme už definovali, teda o aký genóm ide, veľkosť populácie, počet generácií, pravdepodobnosť mutácie, pravdepodobnosť kríženia. Je potrebné nastaviť aj to, podľa čoho bude vyberať vhodných kandidátov. Preto si vytvoríme objekt typu GATournamentSelector. Volič na základe turnaju používa metódu, kde si pomocou rulety vyberie dvoch jedincov a vyberie toho s vyšším skóre. Tento volič častejšie vyberá vyššie ohodnotených jedincov ako RouletteWheelSelector. Toto teda tiež priradíme do genetického algoritmu a ten môžme konečne spustiť. Pre každý genóm zbehne funkcia Objective, kde voláme funkciu Evaluate s hodnotami, ktoré sme získali z genómu. Funkcia Evaluate je funkcia, ktorá využíva ODE. V tejto funkcií sa spustí simulácia. Výsledkom tejto funkcie je fitness, ktoré priradíme na základe toho, ako ďaleko robot došiel. V tejto funkcií si vytvoríme premennú typu dsFunctions, ktorej ako jeden krok nastavíme funkciu simLoop. Funkcia simLoop vytvorí robota a simuluje jeho pohyb. Zároveň sa v nej počíta počet "tikov", teda ako dlho má jedna simulácia bežať. Ak sa tento počet už prekročí, simulácia bude zastavená a vyráta sa fitness pre robota s aktuálnymi parametrami. Táto fitness je výstupom funkcie Evaluate. Hodnoty, ktoré do Evaluate funkcie posielame použijeme pri pohybe robota ako sily, ktoré naňho pôsobia.
Objective function
float
Objective(GAGenome& g) {
GA2DBinaryStringGenome & gg = (GA2DBinaryStringGenome &) g;
int a = 0;
for(int i=0; i<gg.width(); i++){ // vyrobíme číslo a z prvého riadku genómu
a <<= 1;
a += gg.gene(i, 0);
}
int b = 0;
for(int i=0; i<gg.width(); i++){ // vyrobíme číslo b z druhého riadku genómu
b <<= 1;
b += gg.gene(i, 1);
}
int c = 0;
for(int i=0; i<gg.width(); i++){ // vyrobíme číslo c z tretieho riadku genómu
c <<= 1;
c += gg.gene(i, 2);
}
return evaluate((a / 1048576.0), (b / 1048576.0), (c / 1048576.0));
}
Pohyb robota
static double angle = 0;
angle += d1; // budeme zväčšovať uhol o hodnotu d1, ktorú sme dostali z Obejctive funkcie ako a
dBodyAddForce(body[NUM -1], d2+d3,d2-d3,1.5*(sin(angle)+1.0)); // sily pôsobiace na robota v smeroch na x-ovej, y-ovej a z-ovej osi
// d1, d2, d3 sme dostali z Objective funkcie ako a, b, c
Výsledky
Program bol pustený približne 12 hodín. Bol testovaný na populácií o veľkosti 100 a celkovo takto veľkých generácií bolo pustených 85. Na obrázku dobre vidno, že program začal pomerne rýchlo konvergovať a už približne v 40-tej generácií sa dostal k najlepšiemu riešeniu, aké našiel za celý svoj beh. Na x-ovej osi grafu sú čísla 1 až 85, teda vieme určiť, ktorá generácia to bola. Na y-ovej osi grafu sú reálne čísla, ktoré predstavujú vzdialenosť, ktorú prešiel najlepší robot danej generácie.
Ukážky
Najlepší robot z generácie 1, d1 = 0.1166162, d2 = 0.8740978, d3 = 0.8906136, výsledok = 13.5978
Najlepší robot z generácie 8, d1 = 0.1162930, d2 = 0.8566837, d3 = 0.9842405, výsledok = 17.6451
Najlepší robot z generácie 85, d1 = 0.1195879, d2 = 0.9615898, d3 = 0.9914131, výsledok = 19.4745