Difference between revisions of "Spike Prime - Static Wave Generator"
m |
m |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <small>(''[[Spike up Prime Interest in Physics|back to list of projects]]'')</small> | ||
| + | |||
== Let's begin == | == Let's begin == | ||
| − | + | Our world is formed of elementary particles that can also exhibit a form and behavior of waves. In other words, undulation is all around us and the world is built of undulation. And when talking about waves, it's not so much about the wool of sheep. :-) As we will soon see, it's more about the waves a guitar string is making when producing a tone. | |
| + | |||
| + | When energy propagates in the space, it is through undulation. The wavelength (i.e. the distance a single wave occupies in the space) depends on the speed of wave travel and the frequency of undulation. The faster the speed, the longer the distance it can travel in a single period and thus the longer wavelength. The higher frequency of undulation, i.e. a single oscillation takes shorter time, the shorter the wavelength. The speed of wave travel (propagation of the undulation through the environment) depends on the type of the undulation and the properties of the environment. For instance, a visible light (electromagnetic undulation) spreads with the speed of light in the vacuum, but it travels about 40% more slowly through glass - and that is why the eyeglasses work. | ||
| + | |||
| + | When the wave hits an obstacle, it can be reflected back (typically in an inverse phase). The reflected wave travels the space back and adds up with the forthcoming waves in the opposite direction. The reflected wave has about the same speed and the amplitude and thus an interesting phenomenon occurs: a standing wave. With progressing waves, the energy is transmitted in the direction of the wave travel, whereas with standing wave, no energy is transmitted. If the undulation is damped by the environment for instance, we still need to provide the energy to keep the stationary wave alive. | ||
| + | |||
| + | [[Image:standing_wave.gif]] | ||
| + | |||
| + | We will play with mechanical undulation. Take a an elastic string and bind it to something at its end or hold it tight in your hand. We build a robot that will be shaking one end of the string with a modifiable frequency thus forming a wave that travels the string towards the tied end and then reflecting back. If the waves are generated in a proper (fundamental) frequency, the place where the robot fixes the rope happens to be in a quiet position of the stationary wave (node) and the stationary wave will be formed. | ||
== Build == | == Build == | ||
| Line 7: | Line 17: | ||
Model: | Model: | ||
| − | [[Image:spike_stationary_wave.png|model of vehicle| | + | [[Image:spike_stationary_wave.png|model of vehicle|600px]] |
Pictures: | Pictures: | ||
| − | [[Image:spike_stationary_wave.jpg|wave generator|300px]] | + | [[Image:spike_stationary_wave.jpg|wave generator|700px]] |
| + | |||
| + | Alternate construction - a complete model for fixing the string (just an example): | ||
| + | |||
| + | [[Image:spike_stationary_wave_alt1.jpg|alternate model|300px]] | ||
| + | [[Image:spike_stationary_wave_alt2.jpg|alternate model|300px]] | ||
| + | [[Image:spike_stationary_wave_alt3.jpg|alternate model|300px]] | ||
| + | |||
Building instructions: | Building instructions: | ||
| Line 34: | Line 51: | ||
Download: [[Media:stationary_wave.llsp|stationary_wave.llsp]] | Download: [[Media:stationary_wave.llsp|stationary_wave.llsp]] | ||
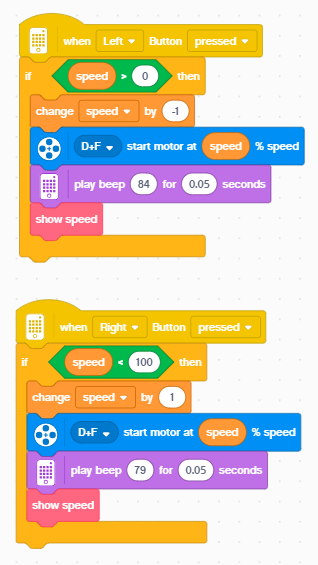
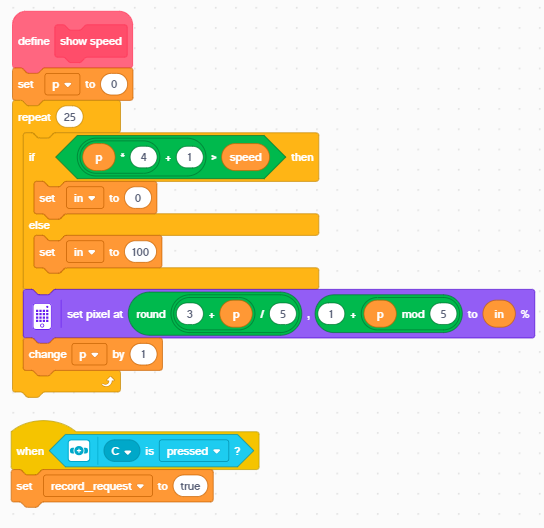
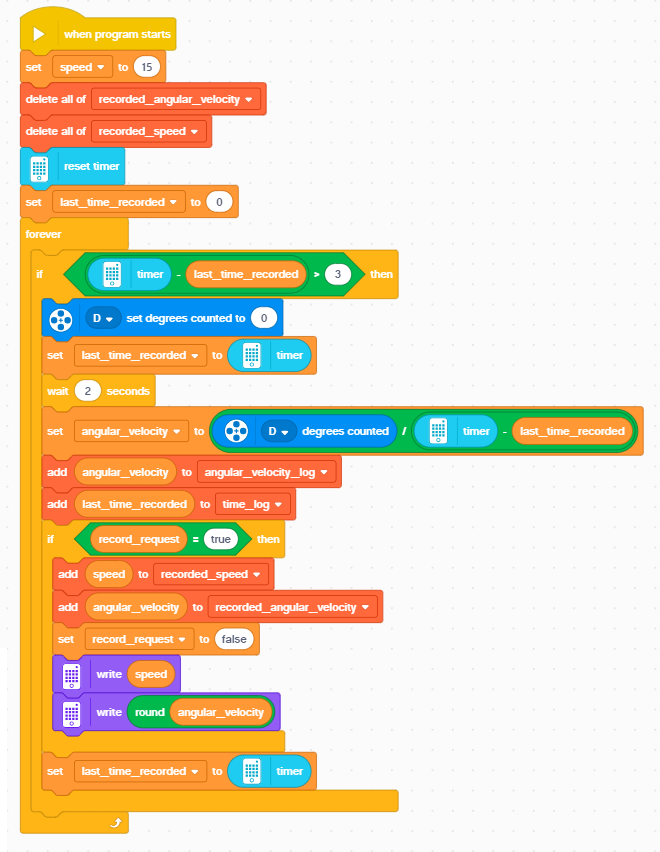
| − | + | After starting the program, you can increase/decrease the speed of the motors by pressing the right/left buttons on the hub. | |
| + | Pressing the attached force sensor causes the current measured motor power and angular velocity to be added to the recording list variables. At the same time, these values are automatically logged every 3 seconds anyway. The current power is visualized on the hub's display - every cell corresponds to a power difference of 4, all LEDs on = 4 * 25 = power 100. The actual frequency will depend on the load that changes with the wave behavior and tension in the string. | ||
| + | |||
| + | |||
| + | == Measure, analyze, think == | ||
| + | <youtube>NlBWS4v6tHs</youtube> | ||
| + | alternate setup: | ||
| − | == | + | <youtube width="width="350" height="700">wxgFm5GNUXs</youtube> |
| − | + | * Use the buttons of the hub to tune the frequency to achieve fundamental frequency and stationary undulation. | |
| + | * Try to find also the second and the third harmonic frequencies - when a stationary wave with multiple nodes (points where the string does not move) will be formed. | ||
| + | * Try to change the length of the string, | ||
| + | * try to change the tension in the string (pull gently) | ||
| + | * Use the button to record the angular velocities. | ||
| + | * Use the "dumpvars" project from the [[Spike_Prime_-_Mathematical_Pendulum|pendulum]] exercise to extract the measured data from the project. | ||
| + | * Calculate the frequencies from the angular velocity. Measure the string length. Determine the speed of the wave travel. | ||
* Make your own recording | * Make your own recording | ||
| Line 52: | Line 81: | ||
== Explore and modify == | == Explore and modify == | ||
| − | * Modify the program so that | + | * Modify the program so that you can browse through the power in a faster way. |
| − | * Modify the model so that . | + | * Modify the model so that the gear ration will be different. Will you get better results? |
== Present == | == Present == | ||
Latest revision as of 15:42, 28 February 2020
Let's begin
Our world is formed of elementary particles that can also exhibit a form and behavior of waves. In other words, undulation is all around us and the world is built of undulation. And when talking about waves, it's not so much about the wool of sheep. :-) As we will soon see, it's more about the waves a guitar string is making when producing a tone.
When energy propagates in the space, it is through undulation. The wavelength (i.e. the distance a single wave occupies in the space) depends on the speed of wave travel and the frequency of undulation. The faster the speed, the longer the distance it can travel in a single period and thus the longer wavelength. The higher frequency of undulation, i.e. a single oscillation takes shorter time, the shorter the wavelength. The speed of wave travel (propagation of the undulation through the environment) depends on the type of the undulation and the properties of the environment. For instance, a visible light (electromagnetic undulation) spreads with the speed of light in the vacuum, but it travels about 40% more slowly through glass - and that is why the eyeglasses work.
When the wave hits an obstacle, it can be reflected back (typically in an inverse phase). The reflected wave travels the space back and adds up with the forthcoming waves in the opposite direction. The reflected wave has about the same speed and the amplitude and thus an interesting phenomenon occurs: a standing wave. With progressing waves, the energy is transmitted in the direction of the wave travel, whereas with standing wave, no energy is transmitted. If the undulation is damped by the environment for instance, we still need to provide the energy to keep the stationary wave alive.
We will play with mechanical undulation. Take a an elastic string and bind it to something at its end or hold it tight in your hand. We build a robot that will be shaking one end of the string with a modifiable frequency thus forming a wave that travels the string towards the tied end and then reflecting back. If the waves are generated in a proper (fundamental) frequency, the place where the robot fixes the rope happens to be in a quiet position of the stationary wave (node) and the stationary wave will be formed.
Build
Model:
Pictures:
Alternate construction - a complete model for fixing the string (just an example):
Building instructions:
Download building instructions:
Download stud.io model:
Program
Download: stationary_wave.llsp
After starting the program, you can increase/decrease the speed of the motors by pressing the right/left buttons on the hub. Pressing the attached force sensor causes the current measured motor power and angular velocity to be added to the recording list variables. At the same time, these values are automatically logged every 3 seconds anyway. The current power is visualized on the hub's display - every cell corresponds to a power difference of 4, all LEDs on = 4 * 25 = power 100. The actual frequency will depend on the load that changes with the wave behavior and tension in the string.
Measure, analyze, think
alternate setup:
- Use the buttons of the hub to tune the frequency to achieve fundamental frequency and stationary undulation.
- Try to find also the second and the third harmonic frequencies - when a stationary wave with multiple nodes (points where the string does not move) will be formed.
- Try to change the length of the string,
- try to change the tension in the string (pull gently)
- Use the button to record the angular velocities.
- Use the "dumpvars" project from the pendulum exercise to extract the measured data from the project.
- Calculate the frequencies from the angular velocity. Measure the string length. Determine the speed of the wave travel.
- Make your own recording
Example result of measurement:
- Perform measurements with your model and discuss in your group what has happened.
Explore and modify
- Modify the program so that you can browse through the power in a faster way.
- Modify the model so that the gear ration will be different. Will you get better results?
Present
- Prepare a short presentation for other groups. Tell others about how your measurement went, what issues did you have to solve. What do they mean and why did they happen?
Additional resources
- Download: stationary_wave - all media files