Difference between revisions of "Filtre"
From RoboWiki
(→Moving Average Filter) |
|||
| Line 4: | Line 4: | ||
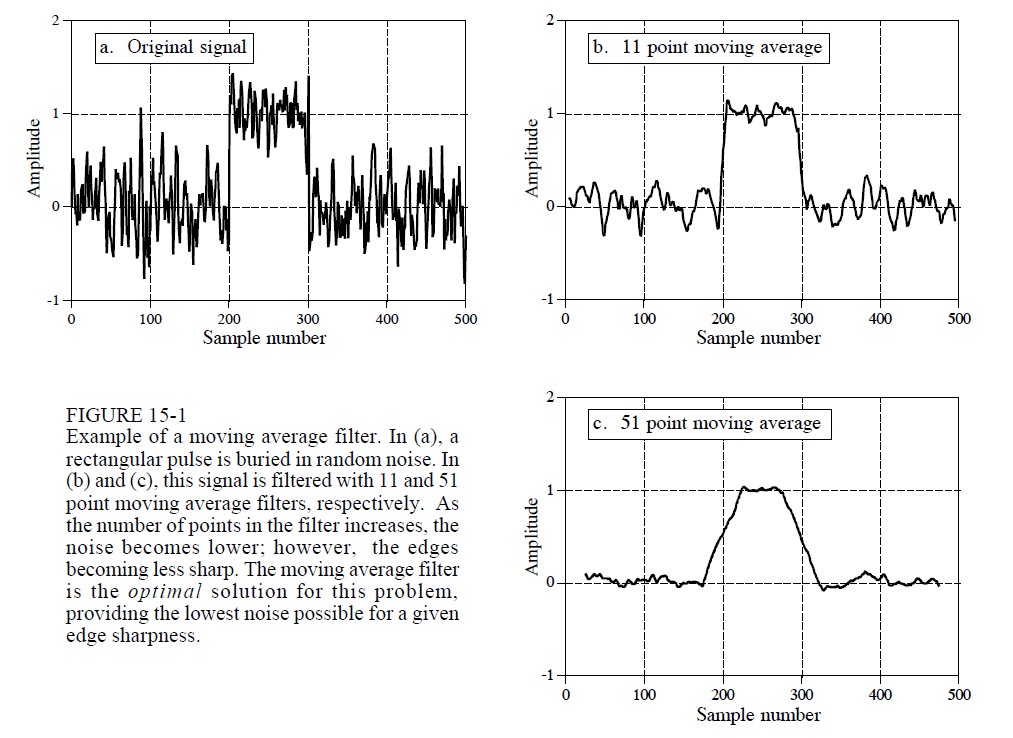
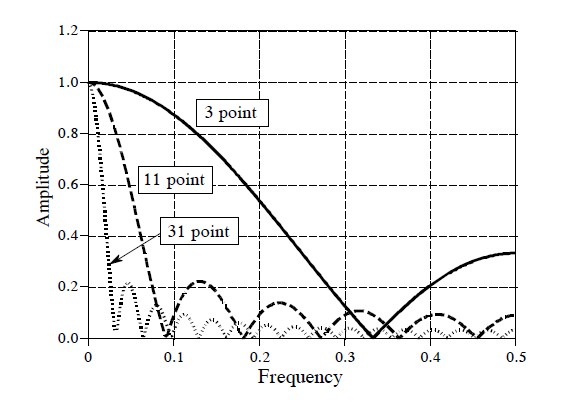
== Moving Average Filter == | == Moving Average Filter == | ||
| + | |||
| + | == Plávajúci priemer == | ||
| + | |||
| + | % Toto je moj vlastny plavajuci priemer | ||
| + | % | ||
| + | % Verzia 1.0 na prvy pokus 5. 6. 2008 R.B. | ||
| + | % | ||
| + | |||
| + | function y = movingaverage (x, M) | ||
| + | |||
| + | % x je vstupny vektor, ktory filtrujeme | ||
| + | % M je rad filtra, kolko clenov priemerujeme | ||
| + | |||
| + | y=[zeros(1,M-1) x]; % predlzime vektor o M-1 nul na zaciatku | ||
| + | % aby sa aj prva hodnota zaratala do priemeru | ||
| + | for i=1 : length(x) | ||
| + | y(i) = sum( y( i : (i+M-1) ) ); % spocitavame M-tice | ||
| + | endfor | ||
| + | |||
| + | y=y/M; % napokon to vydelime | ||
| + | |||
| + | y=y(1:length(x)); % a vektor zasa skratime o ten | ||
| + | % pridavok, lenze na konci | ||
| + | |||
| + | endfunction | ||
| + | |||
| + | |||
| + | [[Media:movingaverage.m|movingaverage.m]] | ||
| + | |||
| + | === Príklad použitia === | ||
| + | |||
| + | % Priklad na pouzivanie MA filtra: | ||
| + | |||
| + | SignalSinus=sin(linspace(1,6*pi,300)) | ||
| + | |||
| + | |||
| + | % Najprv sa pozrime, ako poskodi MA filter povodny harmonicky | ||
| + | % signal pri roznych velkostiach okienka: | ||
| + | |||
| + | plot(SignalSinus); hold on; | ||
| + | plot(movingaverage(SignalSinus,5)); | ||
| + | plot(movingaverage(SignalSinus,25)); | ||
| + | plot(movingaverage(SignalSinus,100)); | ||
| + | |||
| + | |||
| + | % Teraz uz naozaj ideme filtrovat. Vidno, ze ak jed MA filter | ||
| + | % normalny cisty signal mierne tlmi, tuto sa to neprejavi, pretoze | ||
| + | % sum niektore hodnoty rozhodi aj smerom nahor, aj nadol. Takze | ||
| + | % vyfiltrovany sinus je niekedy aj vacsi ako povodny... | ||
| + | |||
| + | clg; | ||
| + | |||
| + | noise = 0 + 0.1 * randn(size(SignalSinus)); % \mu = 0, \sigma = 0.1 | ||
| + | |||
| + | plot(SignalSinus+noise); hold on; | ||
| + | plot(movingaverage(SignalSinus+noise,10),"r"); | ||
| + | plot(SignalSinus,"g"); | ||
| + | |||
| + | |||
| + | |||
| + | % Teraz ideme filtrovat realne data z teplomera: | ||
| + | |||
| + | clg; | ||
| + | data; % nacita vektor temperature s teplotami: | ||
| + | |||
| + | |||
| + | t1 = movingaverage(temperature(:,2)',10); % skus rozlicne M = 10, 30, 100 | ||
| + | plot(t1); | ||
| + | hold on; | ||
| + | plot(temperature(:,2),"g"); | ||
| + | |||
| + | |||
| + | [[Media:MAexample.m|MAexample.m]] | ||
| + | [[Media:data.m|data.m]] | ||
Revision as of 15:25, 18 June 2008
- Java príklady na hrátky so signálmi http://www.dsptutor.freeuk.com/
- Frekvenčná charakteristika: tester sluchu
Moving Average Filter
Plávajúci priemer
% Toto je moj vlastny plavajuci priemer
%
% Verzia 1.0 na prvy pokus 5. 6. 2008 R.B.
%
function y = movingaverage (x, M)
% x je vstupny vektor, ktory filtrujeme
% M je rad filtra, kolko clenov priemerujeme
y=[zeros(1,M-1) x]; % predlzime vektor o M-1 nul na zaciatku
% aby sa aj prva hodnota zaratala do priemeru
for i=1 : length(x)
y(i) = sum( y( i : (i+M-1) ) ); % spocitavame M-tice
endfor
y=y/M; % napokon to vydelime
y=y(1:length(x)); % a vektor zasa skratime o ten
% pridavok, lenze na konci
endfunction
Príklad použitia
% Priklad na pouzivanie MA filtra: SignalSinus=sin(linspace(1,6*pi,300)) % Najprv sa pozrime, ako poskodi MA filter povodny harmonicky % signal pri roznych velkostiach okienka: plot(SignalSinus); hold on; plot(movingaverage(SignalSinus,5)); plot(movingaverage(SignalSinus,25)); plot(movingaverage(SignalSinus,100)); % Teraz uz naozaj ideme filtrovat. Vidno, ze ak jed MA filter % normalny cisty signal mierne tlmi, tuto sa to neprejavi, pretoze % sum niektore hodnoty rozhodi aj smerom nahor, aj nadol. Takze % vyfiltrovany sinus je niekedy aj vacsi ako povodny... clg; noise = 0 + 0.1 * randn(size(SignalSinus)); % \mu = 0, \sigma = 0.1 plot(SignalSinus+noise); hold on; plot(movingaverage(SignalSinus+noise,10),"r"); plot(SignalSinus,"g"); % Teraz ideme filtrovat realne data z teplomera: clg; data; % nacita vektor temperature s teplotami: t1 = movingaverage(temperature(:,2)',10); % skus rozlicne M = 10, 30, 100 plot(t1); hold on; plot(temperature(:,2),"g");